جدول المحتويات
التبرير الاستقرائي والتخمين هما استراتيجيتان أساسيتان في التفكير المنطقي والرياضي، ولكن كل منهما يعتمد على منهج مختلف للوصول إلى استنتاجات، وغالبًا ما يكون التبرير الاستقرائي مقدمة للتخمين، وبمجرد ملاحظة نمط معين من خلال الاستقراء، يمكن للمرء أن يخمن قاعدة أو نظرية عامة ثم يحاول إثباتها.
بحث عن التبرير الاستقرائي والتخمين
يُدرج فيما بحث عن التبرير الاستقرائي والتخمين كامل العناصر:[1]
مقدمة بحث عن التبرير الاستقرائي والتخمين
يُعد التفكير المنطقي جزءًا أساسيًا من الحياة اليومية والعلوم المختلفة، إذ يعتمد على بناء الاستنتاجات واتخاذ القرارات بطريقة منهجية، ومن بين الأساليب المستخدمة في هذا السياق نجد التبرير الاستقرائي والتخمين، اللذين يُعتبران ركيزتين أساسيتين في علم الرياضيات والمنطق.
في هذا البحث سنستعرض مفهوم كل من التبرير الاستقرائي والتخمين، وأهمية كل منهما في العلوم الرياضية، وكيفية استخدامهما في بناء القواعد والنظريات، كما سنناقش التحديات التي تواجه كل منهما، وأمثلة عملية من الواقع والمجالات العلمية المختلفة.
ما هو تعريف التبرير الاستقرائي
التبرير الاستقرائي هو أحد فروع علم الرياضيات، ويعتمد على التجارب المتكررة للوصول إلى نتائج منطقية، ويستند هذا التبرير إلى ملاحظة استمرار الأحداث بنفس الطريقة والنمط في ظل عدم تغير الظروف المحيطة، مما يمكن الباحث من استخلاص نتائج مدروسة ومبنية على أسس علمية، ويعتمد التبرير الاستقرائي على تجميع الملاحظات والتجارب لاستخلاص تعميمات واسعة من حالات محددة، وهو نوع من المنطق الذي يبدأ فيه الباحث من المواقف الخاصة ويعممها لتشمل حالات أوسع.
من خلال هذا المنطق، يقوم الباحث بملاحظة عدد كبير من الحالات، ثم يميز نمطًا معينًا قبل أن يقوم بالتعميم وإنتاج نظريات أو تفسير أخرى، هذا النهج يرتبط أيضًا بمفهوم التخمين حيث يُعتمد عليه في البحث العلمي للوصول إلى نتائج.
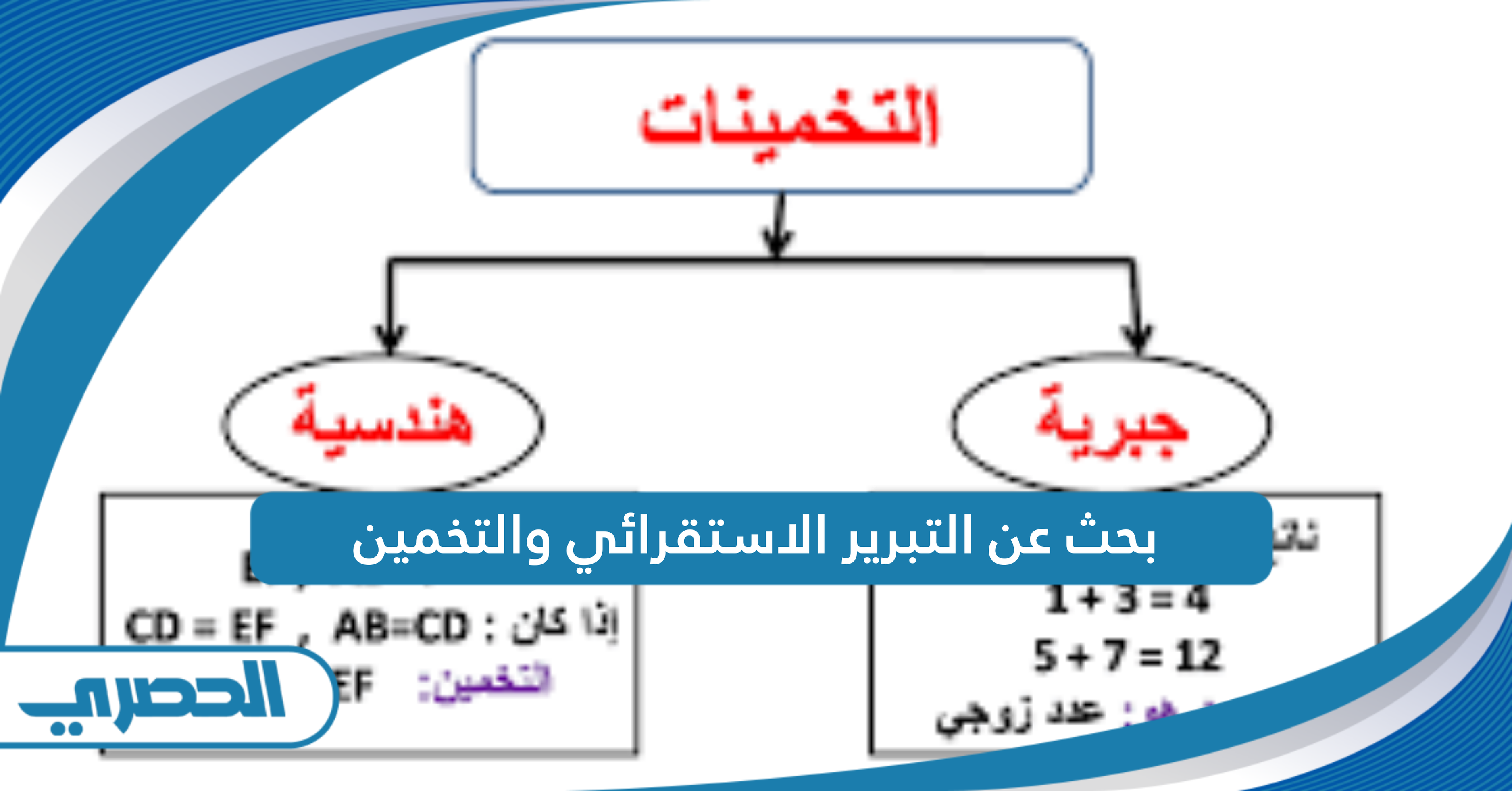
ما هو تعريف التخمين
التخمين هو عبارة عن استنتاج نهائي يتم الوصول إليه من خلال عملية التبرير الاستقرائي، ويعبر عن قاعدة أساسية تُبنى عليها الملاحظات، رغم أنها لم تُثبت بشكل قاطع بعد، وفي الرياضيات يُعتبر التخمين مجموعة من الفرضيات التي يتم من خلالها محاولة حل المعطيات والمعلومات المتاحة خلال البحث، ويُعد التخمين أداة هامة عند دراسة الخيارات الأولية، حيث يستند إلى حقائق مثبتة أو مصادر معتمدة، ولا يعتمد على الحظ أو الصدفة.
من الجدير بالذكر أن التخمين الرياضي يعتمد بشكل رئيسي على المنطق، وليس العشوائية، فهو نتيجة مباشرة للتبرير الاستقرائي، حيث يشتركان في الأسس والمنهجية ذاتها، وفي كلاهما يُبنى التحليل على نفس النظريات والرؤى، ويُستخدم مصطلح التخمين للإشارة إلى الاستنتاج النهائي الذي يتم التوصل إليه عبر هذه العملية.
اهمية التبرير الاستقرائي والتخمين في حياتنا
يُدرج فيما يلي اهمية التبرير الاستقرائي والتخمين في حياتنا:[2]
- يمكن استخدام التبرير الاستقرائي في الحياة اليومية لكل من الطالب والمعلم، فهو ليس مجرد علم نظري يُدرس في المدارس والجامعات، بل يمكن تطبيقه للوصول إلى نتائج هامة في الحياة.
- تساعد النظريات الرياضية في تحسين صفاء الذهن وتعزيز القدرة على التفكير بشكل منطقي ومتوازن، مما يمكّن الفرد من توقع الأحداث المستقبلية والتأهب نفسيًا للتعامل مع مختلف التحديات.
- من خلال ممارسة التبرير الاستقرائي، يتعلم الطالب كيفية الغوص في التفاصيل الدقيقة للأحداث وتحليلها بعمق، وهذا يسهم في تحسين قدرته على التفكير بشكل مميز، وتمكنه من اختيار الحلول الأنسب بناءً على توقعات دقيقة ناتجة عن التفكير المنطقي.
- تُبنى الحياة الشخصية للفرد الدارس على أساس العقلانية في اتخاذ القرارات بشأن جميع جوانب الحياة، وهو ما يبرز أهمية التبرير الاستقرائي في الرياضيات. فالاستناد إلى آليات التفكير الاستقرائي والتخمين يعزز فهم الفرد للتداعيات والتطورات التي يواجهها في حياته اليومية.
- يعد التبرير الاستقرائي أداة رئيسية تدعم المنهج العلمي، حيث يجمع الباحثون البيانات الأساسية من خلال الملاحظة والتجربة، ثم يضعون فرضيات بناءً على تلك البيانات ويختبرونها على نطاق أوسع.
- الفرضيات تعد خطوة أساسية في عملية الاستنتاج الاستقرائي، ويسهم التخمين في استكشاف مسارات أخرى للبحث والاستدلال.
- يمكن اعتبار التفكير الاستقرائي مكونًا أساسيًا في الحياة الأكاديمية لكل من الطالب والمعلم، كما يسهم التبرير الاستقرائي والتخمين في تقديم خدمات مهمة للعاملين في المجالات الاقتصادية والتجارية، مثل رجال الأعمال وأصحاب الشركات، حيث تكون فوائده واضحة في مجالات مثل أسواق البورصة والأسهم.
طريقة حل مسائل التبرير الاستقرائي و التخمين
لحل مسائل التبرير الاستقرائي والتخمين بطريقة فعالة يمكن اتباع الخطوات التالية:[3]
- فهم المسألة جيدًا:
- قراءة المسألة بتمعن لتحديد البيانات والمعلومات المعطاة، وتحديد ما هو مطلوب حله أو الوصول إليه، ويجب أن يفهم الهدف من المسألة بوضوح.
- جمع الملاحظات أو المعطيات
- في التبرير الاستقرائي، البدأ بجمع الملاحظات أو المعطيات المتاحة، وهذه المعطيات قد تكون عبارة عن أرقام، أنماط، أمثلة أو مواقف متكررة.
- الحرص على تسجيل الملاحظات بدقة حتى يمكن تحليلها لاحقًا.
- البحث عن الأنماط
- بعد جمع الملاحظات تحليلها للبحث عن أي نمط أو علاقة بين البيانات، وقد يكون هذا النمط متكررًا أو يتزايد بطريقة معينة (على سبيل المثال: الأعداد المتتابعة أو تسلسل منطقي).
- هذا هو الجزء الأساسي في التبرير الاستقرائي، حيث يسعى لاكتشاف النمط الذي يمكن الاعتماد عليه في استنتاج النتائج.
- تكوين التخمين
- بعد تحديد النمط أو العلاقة، وتكوين فرضية أو تخمين حول المسألة، وهذا التخمين يمثل الاستنتاج بناءً على الأنماط المكتشفة.
- التخمين قد يكون معتمدًا على مبدأ متكرر، قاعدة حسابية، أو سلوك معين للبيانات.
- اختبار التخمين
- تطبيق التخمين أو الفرضية التي تم التوصل إليها على بيانات جديدة أو أمثلة إضافية للتأكد من صحتها، وهذا يساعد في التحقق من صحة الاستنتاج وتأكيد أن النمط المكتشف ينطبق على جميع الحالات المشابهة.
- إذا كان التخمين صحيحًا، يمكن الانتقال إلى الخطوة التالية؛ وإذا لم يكن كذلك، يجب مراجعة الفرضية وتعديلها بناءً على المعلومات الجديدة.
- تعميم الحل
- إذا كان التخمين صحيحًا ويمثل حل المسألة بشكل عام، وتعميم الحل أو الفرضية لتشمل الحالات المشابهة الأخرى، ويمكن استخدام الاستنتاج المستخلص لحل مسائل أخرى تتبع نفس النمط.
- التوثيق والتأكد من الحل النهائي
- تدوين الاستنتاجات النهائية بشكل واضح ومنظم، وتأكد من صحة الحل النهائي.
- مثال تطبيقي:
- المسألة: لاحظت أن متسلسلة الأرقام (3، 6، 12، 24، …) تتزايد، فما هو الرقم التالي في المتسلسلة؟
-
- فهم المسألة: نحتاج إلى تحديد النمط الذي تتبعه المتسلسلة لتحديد الحد التالي.
- جمع الملاحظات: المتسلسلة هي: 3، 6، 12، 24.
- البحث عن الأنماط: نلاحظ أن كل عدد يتم ضربه في 2 للحصول على العدد الذي يليه (3 × 2 = 6، 6 × 2 = 12، 12 × 2 = 24).
- تكوين التخمين: التخمين هنا هو أن النمط يعتمد على مضاعفة العدد السابق × 2.
- اختبار التخمين: إذا طبقنا نفس النمط، سيكون الحد التالي هو 24 × 2 = 48.
- تعميم الحل: بناءً على هذا النمط، يمكننا الاستنتاج بأن الحد التالي هو 48.
- التأكد: الحل يتماشى مع نمط مضاعفة الأعداد، وهو صحيح.
خاتمة بحث عن التبرير الاستقرائي والتخمين
في ختام هذا البحث عن التبرير الاستقرائي والتخمين، يتضح لنا مدى أهمية هذه الأدوات الفكرية في تطوير التفكير المنطقي والتحليلي، فالتبرير الاستقرائي لا يقتصر فقط على المجال الأكاديمي أو الرياضي، بل يمتد ليشمل حياتنا اليومية، حيث يساعدنا في فهم الأنماط، توقع النتائج، واتخاذ قرارات مدروسة، أما التخمين فيمنحنا القدرة على استكشاف احتمالات جديدة واختبار فرضيات تساهم في تطوير حلول مبتكرة.
بحث عن التبرير الاستقرائي والتخمين PDF
يمكن الوصول إلى بحث عن التبرير الاستقرائي والتخمين بصيغة PDF مباشرةً “من هنا“، حيث بفضل التبرير الاستقرائي والتخمين، يمكن للطلاب والباحثين ورجال الأعمال استخدام هذه المهارات للتوصل إلى حلول منطقية وفعالة.
بحث عن التبرير الاستقرائي والتخمين doc
يمكن تحميل بحث عن التبرير الاستقرائي والتخمين بصيغة doc مباشرةً “من هنا“، إذ يُعد علم الرياضيات من أقدم العلوم التي اكتشفها الإنسان نتيجة لحاجته الملحّة إليها في الحياة اليومية، وقد أصبح من الأساسيات التي تستحق الاهتمام الكبير.
المراجع
- ^ youtube.com , رياضيات 1-1 (1-1 التبرير الاستقرائي والتخمين , 18/10/2024
- ^ varsitytutors.com , Inductive Reasoning , 18/10/2024
- ^ iep.utm.edu , Deductive and Inductive Arguments , , 18/10/2024


















اترك تعليقاً